| Lexikon | Formler | Terminologi länkar | Böcker |
Gästbok |
Nedladdning |
|
| Linjära ekvation Linjära ekvationssystem Andragradsekvation Tredjegradsekvation |
Algebraiska ekvationslösningar |
Identitet Ekvation Grafiska ekvationslösningar Numeriska lösningar |
En lösning (en rot) till en ekvation är ett sådant värde på den obekanta resp. sådana värden på de obekanta som innebär att likheten (mellan ekvationens bägge led) gäller.
Att (upp)lösa en ekvation betyder att bestämma alla värden, som satisfiera honom, och han är upplöst, när den obekanta ensam finns på ena sidan om likhetstecknet och bara bekanta på den andra.
Existens av en lösning (rot) och antalet rötter beror på bland vilka tal söker vi lösningar.
(t.ex. komplextal, reellt tal, rationellt tal, heltal).
Exempel: x² + 1 = 0 har ingen reell lösning.
För att lösa en ekvation, måste man finna alla lösningar (rötter).
Utan att rubba ledernas likhet kan man till dem båda addera och från båda subtrahera samma tal eller uttryck.
I ekvationen x - 3 = 5 adderas 3 på båda sidor. Då får man: x = 8
I ekvationen 2x + 1 = x - 1 subtraheras (x + 1) från båda sidor: x = - 2Utan att rubba ledernas likhet kan man multiplicera och dividera dem båda med samma tal eller uttryck om värdet av uttrycket (talet) är ej noll.
Multiplikation med 4 ger x = 12.
Förkorta bort ett uttryck
I en ekvation kan man förkorta bort (dividera med) ett uttryck, som innehåller obekanta (x), under förutsättning, att man samtidigt sätter detta uttryck lika med 0, och låter det bestämma en rot till ekvationen.Exemplar:
Lös ekvationen:
(x + 2)(x - 5) = x + 2
Vi förkortar här med x + 2 och sätter samtidigt detta uttryck lika med 0. Den givna ekvationen ersättes då med två nya ekvationer:
1) x + 2 = 0
2) x - 5 = 1
Vi får x1 = -2, x2 = 6
Lös ekvationen:
sin(x)(cos(x) + 2) = sin(x)
1) sin(x) = 0
2) cos(x) + 2 = 1
x1 = 0, x2 = π
Enkel ekvation eller linjär ekvation
(ekvation av första graden med en obekant)
Rekommenderade moment:
1. Ta bort nämnare (bråket bortskaffas)
2. Ta bort parenteser, inom vilka den obekanta förekommer
3. Med addition och subtraktion bortskaffas termer så, att alla termer i vilka den obekanta ingår kommer på ena sidan och bara bekanta på den andra.
Linjära ekvationssystem
(ekvationer av första graden med flera obekanta)
Linjär sägs en ekvation vara om den eller de obekanta förekommer endast i första potensen.
elimination (vid lösandet av ekvationssystem) är en metod att bortskaffa en av de obekanta och samtidigt reducera antalet ekvationer med ett.
eliminera = avlägsna, utesluta
reducera = minska
3 x + y = 5
y = 2 x
_________________
3 x + ( 2 x) = 5 ![]() 5 x = 5
5 x = 5
Lösningen till ett ekvationssystem med två obekanta
Substitutionsmetod: (insättning)
1. Lös ut en obekant i en av ekvationerna. (x eller y)
2. Sätt in detta uttryck i den andra ekvationen.
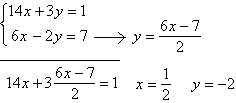
Substitution är den operation, varigenom i ett uttryck eller en ekvation en storhet ersättes genom en annan. Genom substitutionen ändras uttryckets form i enlighet med matematiskt giltiga lagar, och substitutionen är i allmänhet avsedd att förenkla uttrycket eller göra det lämpligare för den behandling, varom fråga är. Om t. ex. det givna uttrycket är x² + 2xy + y² och u - y substitueras för x, övergår på det sättet uttrycket till den enklare formen u². Substitutionerna är av stor vikt vid lösning av många ekvationer.
Additionsmetod:
1. Multiplicera vardera ekvationen med lämpliga tal, så att koefficienterna för x (eller y) blir motsatta tal.
2. Addera ekvationerna ledvis så att x-termerna (eller y-termerna) försvinner.
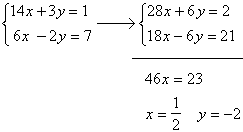
Allmänna lösningen:
Låt de två räta linjernas ekvationer vara
| ax + by + c = 0 | |
| dx + ey + f = 0 |
Lösning av ekvationssystem med determinanter
Cramers regler
En metod att lösa linjära ekvationssystem med användande av determinanter.
På samma sätt som här nedan för 3 obekanta görs med system med ett godtyckligt antal obekanta.
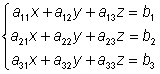
Man får om D ≠ 0:
![]() ;
; ![]() ;
; ![]() .
.
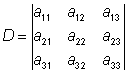 ;
; 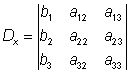 ;
; 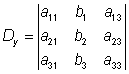 ;
; 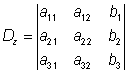 .
.Om D = 0, så är en av de tre ekvationerna en följd av de andra, varför det då ej finns någon entydigt bestämd lösning till systemet. Då finns det däremot lösningar till det homogena systemet: (utom den triviala lösningen x = y = z = 0)
trivialt (i matematiken) = självklart
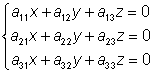
För ett homogent ekvationssystem gäller följande sats: Den homogena ekvation har lösningar (andra än x = y = z = 0) om och endast om D = 0.
Ett linjärt ekvationssystem är homogent om högerledet endast består av nollor.T ex fås lösningen till ekvationssystemet
enlig Cramers regel till
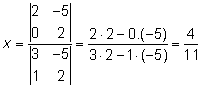
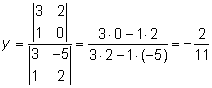
Ekvationer av andra graden med en obekant
Allmän form (kanonisk form):
En ekvation av andra graden är av formen (eller kan förenklas till formen)
ax² + bx + c = 0 och a ≠ 0
Kanonisk (regelrätt, mönstergill) form i matematiken är den mest standardenlig, konventionell och logisk form.
Normalform:
Division med koefficienten för x² reducerar ekvationen till normalformen:
x² + px + q = 0 (p = b/a och q = c/a)
Om en ekvation av andra graden, saknar förstagradsterm (p = 0), kan den skrivs på formen:
x² = a
Om a > 0, har denna ekvationen två reella rötter,
nämligen x1 = ![]() och x2 = -
och x2 = - ![]()
Om a = 0, har ekvationen endast roten x1 = x2 = 0.
0m a < 0, har ekvationen inga reella rötter.
Om en ekvation av andra graden saknar den konstanta termen (q = 0), kan den skrivas på formen
x² + px = 0
Om man bryter ut faktorn x får man
x(x + p) = 0
Här är en produkt som är noll.
Ekvationer två reella rötter: x1 = 0 och x2 = - p.
Kvadratkomplettering
Vi antar, att ekvationen är skriven på normalformen:
x2 + px + q = 0.
Eftersom
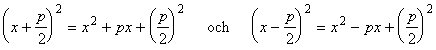
blir uttrycken x² + px och x² - px
jämna kvadrater efter addition av ![]()
Man skall alltså lägga till kvadraten av halva koefficienten för x.
| Ex 1. |
Ex 2. |
||
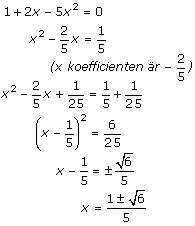 |
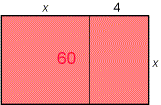 |
x² + 4x - 60 = 0 x(x + 4) = 60 |
|
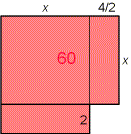 |
x² + 2x +2x =(x + 2)² -2² = 60 |
||
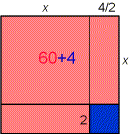 |
x² + 2·2x + 2² =(x + 2)² = 64 x + 2 = ±8 x1 = 6; x2 = -10 |
||
Lösningsformeln för andragradsekvationen
| ekvation är skriven på | formel för rötterna |
| x² + px + q = 0 | 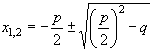 |
| ax² + bx + c = 0 |
Uttrycket D = b² - 4ac kallas för ekvationens diskriminant. Om D > 0, har ekvationen två reella, olika rötter. Om D = 0, har ekvationen två reella, lika rötter. Om D < 0, saknar ekvationen reella rötter. |
Samband mellan rötter och koefficienter till en andragradsekvation.
För en andragradsekvation, skriven i normalform x² + px + q = 0
gäller:
Om rötterna betecknas med x1 och x2, är
| rötternas summa: | x1 + x2 = - p |
| rötternas produkt: | x1 · x2 = q |
Bevis: En ekvation, vars rötter är x1 och x2, kan skrivas
Ekvationer av tredje graden med en obekant
Tredjegradsekvation (kubisk ekvation) i kanonisk form
ax³ + bx² + cx + d = 0 och a ≠ 0
eller (delas med a och istället x införts variabeln ![]() )
)
y³ + 3py + 2q = 0
där![]() och
och ![]()
Uttrycket D = q² - p³ kallas för diskriminant för tredjegradsekvationen.
Om D > 0, har ekvationen en reell, och två konjugata komplexa rötter.
Om D = 0, har ekvationen två reella rötter och minst två av de är lika.
Om D < 0, har ekvationen tre olika reella rötter.
Cardano formel för lösning av tredjegradsekvationer (y³ + 3py + 2q = 0)
y1 = u + v, y2 = ε1u + ε2v, y3 = ε2u + ε1v
där![]() ,
, ![]()
![]()
Egenskaper av tredjegrads ekvationernas rötter:
![]()
![]()
![]()
Falska rötter
Vid lösning av ekvationer och ekvationssystem dyker det ibland upp s. k. falska rötter.
Exempel 1. Lös ekvationen ![]()
Multiplicerar man här korsvis, erhålles ekvationen x² - 1 = 3x - 3,
som ger rötterna x1 = 1 och x2 = 2. Roten x1 = 1 är falsk, ty uttrycket
![]() är inte definierad för x = 1. Man undgår den falska roten,
om man först förkortar bråket i vänstra ledet med (x - 1).
är inte definierad för x = 1. Man undgår den falska roten,
om man först förkortar bråket i vänstra ledet med (x - 1).
Exempel 2. Lös ekvationen ![]() .
.
Genom att multiplicera korsvis erhålles förutom den rätta roten x = 2 den falska x = 1.
Här undgår man den falska roten, om man multiplicerar med den minsta gemensamma nämnaren, vilken här är (x + 1)(x - 1).
Av dessa exempel framgår hur olämpligt det är att begagna korsvis multiplicering.
Många gånger är det lämpligt att gardera sig mot falska rötter av denna typ genom att från början utesluta nämnarens nollställen. I ovanstående exempel skriver man då (x2 - 1) ≠ 0; x ≠ ± 1.
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |