WolframAlpha Lexikon Formler Terminologi länkar Böcker

Gästbok
Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö     
Klicka på någon av bokstäverna
 Nedladdning

Fält, vektorfält

Fält i matematiken och fysiken är en rymd i vilken varje punkt tilldelas en storhet.
Exemplar: vektorfält, elektriskt fält, magnetiskt fält, temperaturfält, gravitationsfält.

Skalärfält, gradient

I ett skalärfält svarar till varje punkt (x, y, z) en skalär storhet U(x,y,z), som vanligt är en funktion av lägeskoordinaterna.
Exempel: Det elektriska potentialfältet.
Ytor som innehåller punkter med samma värde på U, kallas nivåytor (i elektriskt fält ekvipotentialytor).

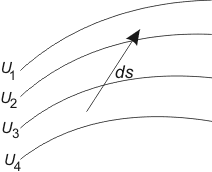
I figur är i ett tvådimensionellt fall olika nivålinjer dragna, och vi söker ett uttryck för ändringen dU i U för en förflyttning ds. För olika riktningar av ds får vi olika värden på dU, vilket innebär att har olika värden i olika riktningen. Eftersom U är en funktion av (x, y, z), kan vi sätta:

Detta uttryck har samma utseende som skalära produkten av två vektorer. dU kan alltså betraktas som produkten av vektorerna grad U och ds, där grad U definieras enligt:

då kan skrivas:
dU = ds·grad U

Lägges vektorn ds utmed en nivåyta, blir enligt definitionen på nivåyta dU = 0. För att ekvationen ska satisfieras måste i detta fall grad U vara vinkelrät mot ds, varav följer att grad U är en vektor, som är vinkelrät mot nivåytorna.

U säges vara potentialen till grad U.

Om vi har E = grad U, gäller för linjeintegralen mellan två punkter 1 och 2:

oberoende av integrationsvägen. För sluten integrationsväg gäller:

Definition enligt:

i kartesiska koordinater:
i sfäriska koordinater:
i cylindriska koordinater

Vektorfält, divergens

Ett vektorfält är ett område, där till varje punkt (x,y,z) svarar en vektor V(x,y, z). Ett flöde, av vätska, gas, elektroner eller annat, kan beskrivas med ett vektorfält

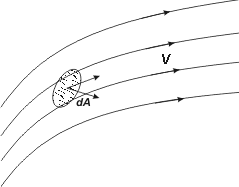I en strömmande vätska bildar hastighetsvektorerna hos vätskans småpartiklar ett vektorfält.
I en strömmande vätska med hastighetsvektorn V tänker vi oss en liten yta dA, vars normal bildar vinkeln (V, dA) med vektorn V.
Genom ytan kommer att strömma en vätskemängd, som uttryckes genom:

V·dA·cos (V·dA) = V·dA

Varav flödet genom arean A är: Φ = V·dA

Vi tänker oss en volym V i vätskan och betecknar med V·dA den totala utåtströmmande vätskemängden. I en vanlig inkompressibel vätska måste denna integral vara noll, då lika mycket vätska måste strömma in i volymen som det strömmar ut (integralen har lika stora negativa som positiva bidrag). Vi kan emellertid tänka oss att det finns källor av vätsketillförsel inom volymen, och vi vill ha en beteckning för hur stor denna vätsketillförsel är. Vätsketillförseln per volymsenhet kallas divergensen (eller källstyrkan) av vektor V, och vi erhåller ekvationen:

Detta samband, som kallas Gauss sats, gäller för alla vektorfält, och innebär att antalet fältlinjer för vektor V, som börjar i en volym, är lika med ytintegralen av de utåtgående fältlinjerna från volymen om fältet är divergensfritt (med annat ord källfritt, solenoialt). Definition enligt:

i kartesiska koordinater:
i sfäriska koordinater:
i cylindriska koordinater:

Vektorfält, rotation

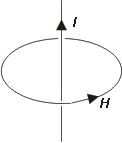
I omgivningen av en lång, rak ledare, i vilken flyter en elektrisk ström, kan lätt påvisas "magnetiska kraftlinjer" med hjälp av en liten kompassnål, som ställer sig i kraftlinjeriktningen. Kraftlinjärna bildar slutna cirklar kring strömbanan.

Rotationen (rot V, eng curl V) av en vektor (i vektorfält) är en vektor som anger vridningsstyrkan och vridningens riktning

Vi tänker oss en yta placerad i vektorfältet V och betraktar linjeintegralen av V längs ytans randkurva. Linjeintegrälen dividerar vi med ytelementets yta Δf och definierar detta som en vektor riktad längs ytans normal. (Normalens riktning sammanhänger med integrationsriktningen enligt skruvregeln.) Vid gränsövergången Δf → 0 är denna vektor komposanten av rot V i normalens riktning, dvs:
Som exempel härleder vi uttrycket för z-komposanten av rot V. Ytelementet kommer därvid att ligga i xy-planet och utgöres av en rektangel med sidorna dx och dy.
Med den i fig angivna integrationsriktningen erhålles linjeintegralen:

Vx(x,y,z)dx + Vy(x+dx,y,z)dy - Vx(x,y+dy,z)dx - Vy(x,y,z)dy =

Den omslutna ytan är dxdy, varför vi erhåller enligt definitionen:

Fullständiga definitionen för rot V blir:

i kartesiska koordinater:
i sfäriska koordinater:
i cylindriska koordinater:

Ett fält, där rotationen överallt är noll, kallas virvelfritt.
Ett vektorfält, där rot V ≠ 0, kallas för virvelfält. I detta fält kan man inte bilda någon gradientfunktion.

Nabla- och Laplaceoperator

Nablaoperatorn (Hamiltonoperatorn) införes för att få ett förkortat beteckningssätt.
-definieras i kartesiska koordinater:

Med denna operator erhålles uttrycken:




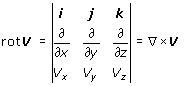
Δ kallas Laplaces operator, och lyder:

av Bruno Kevius
All kopiering tillåten!   
 Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna